Nguyên hàm là chuyên đề quan trọng trong Giải tích Toán 12, thường xuyên xuất hiện trong các kỳ thi đại học. Vậy bảng các công thức nguyên hàm nào cần ghi nhớ? Hãy cùng BangNguyenHam tìm hiểu bảng công thức từ cơ bản đến nâng cao và các phương pháp giải bài tập nguyên hàm qua bài viết sau!
1. Nguyên hàm là gì?
Nguyên hàm là một khái niệm quan trọng trong Giải tích, dùng để tìm một hàm số ban đầu từ đạo hàm của nó.
Cụ thể:
Định nghĩa: Cho hàm số f xác định trên K với K là một khoảng, một đoạn hay một nửa khoảng. Hàm số F được gọi là một nguyên hàm của f trên K nếu: F'(x) = f(x), ∀x ∈ k
Chú ý quan trọng
Chú ý 1:

Chú ý 2:

Các tính chất cơ bản:
- $\left( {\int {f\left( x \right)dx} } \right)’ = f\left( x \right)$
- $\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} $ với k ≠ 0
- $\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} + \int {g\left( x \right)dx} $
- $\int {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} – \int {g\left( x \right)dx} $
2. Bảng các công thức nguyên hàm cần nhớ
2.1 Công thức quan trọng
- Công thức nguyên hàm toàn phần: $\int {udv} = uv – \int {vdu} $
- Công thức biến đổi số: $\int {f\left[ {u\left( x \right)} \right]u’\left( x \right)dv} = f\left[ {u\left( x \right)} \right] + C$
2.2 Công thức nguyên hàm cơ bản

2.3 Công thức nguyên hàm nâng cao

2.4 Bảng công thức nguyên hàm mở rộng

2.5 Nguyên hàm của hàm số lượng giác

3. Các dạng bài tập Nguyên Hàm
Phần Nguyên hàm trong Toán lớp 12 bao gồm các dạng bài tập chọn lọc thường xuất hiện trong đề thi THPT Quốc gia
Dạng 1: Tìm nguyên hàm của hàm số lũy thừa

Dạng 2: Tìm nguyên hàm của hàm số lượng giác
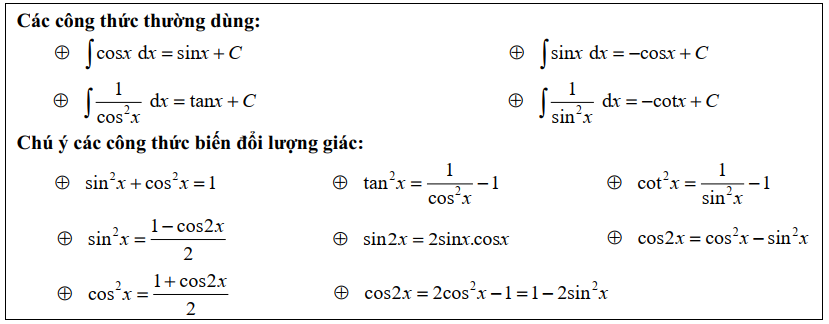
Dạng 3. Tìm nguyên hàm chứa căn thức
Muốn tìm được nguyên hàm của hàm số có chứa căn thức thì em chỉ cần thuộc bảng các công thức nguyên hàm căn thức dưới đây

4. Bài tập
4.1 Bài tập tự luận
Bài tập 1. Tìm:
a) \(\int {{{\left( {x – 2} \right)}^2}dx} \);
b) \(\int {\left( {x – 1} \right)\left( {3{\rm{x}} + 1} \right)dx} \);
c) \(\int {\sqrt[3]{{{x^2}}}dx} \);
d) \(\int {\frac{{{{\left( {1 – x} \right)}^2}}}{{\sqrt x }}dx} \).
Lời giải
a) \(\int {{{\left( {x – 2} \right)}^2}dx} = \int {\left( {{x^2} – 4{\rm{x}} + 4} \right)dx} = \frac{{{x^3}}}{3} – 2{{\rm{x}}^2} + 4{\rm{x}} + C\).
b) \(\int {\left( {x – 1} \right)\left( {3{\rm{x}} + 1} \right)dx} = \int {\left( {3{{\rm{x}}^2} – 2{\rm{x}} – 1} \right)dx} = {x^3} – {x^2} – x + C\).
c) \(\int {\sqrt[3]{{{x^2}}}dx} = \int {{x^{\frac{2}{3}}}dx} = \frac{{{x^{\frac{5}{3}}}}}{{\frac{5}{3}}} + C = \frac{3}{5}{x^{\frac{5}{3}}} + C = \frac{3}{5}x.\sqrt[3]{{{x^2}}} + C\).
d) \(\begin{array}{l}\int {\frac{{{{\left( {1 – x} \right)}^2}}}{{\sqrt x }}dx} = \int {\frac{{{x^2} – 2{\rm{x}} + 1}}{{{x^{\frac{1}{2}}}}}dx} = \int {\left( {{x^{\frac{3}{2}}} – 2{{\rm{x}}^{\frac{1}{2}}} + {{\rm{x}}^{ – \frac{1}{2}}}} \right)dx} = \frac{{{x^{\frac{5}{2}}}}}{{\frac{5}{2}}} – \frac{{2{{\rm{x}}^{\frac{3}{2}}}}}{{\frac{3}{2}}} + \frac{{{{\rm{x}}^{\frac{1}{2}}}}}{{\frac{1}{2}}} + C\\ = \frac{2}{5}{x^{\frac{5}{2}}} – \frac{4}{3}{{\rm{x}}^{\frac{3}{2}}} + 2{{\rm{x}}^{\frac{1}{2}}} + C = \frac{2}{5}{x^2}\sqrt x – \frac{4}{3}{\rm{x}}\sqrt x + 2\sqrt x + C\end{array}\)
Bài tập 2. Tìm:
a) \(\int {\left( {{5^x} + 1} \right)\left( {{5^x} – 1} \right)dx} \);
b) \(\int {{e^{ – 0,5{\rm{x}}}}dx} \);
c) \(\int {{2^{x – 1}}.{5^{2{\rm{x}} + 1}}dx} \).
Lời giải
a) \(\int {\left( {{5^x} + 1} \right)\left( {{5^x} – 1} \right)dx} = \int {\left( {{5^{2x}} – 1} \right)dx} = \int {\left( {{{25}^x} – 1} \right)dx} = \frac{{{{25}^x}}}{{\ln 25}} – x + C = \frac{{{{25}^x}}}{{2\ln 5}} – x + C\).
b) \(\int {{e^{ – 0,5{\rm{x}}}}dx} = \int {{{\left( {{e^{ – 0,5}}} \right)}^x}dx} = \frac{{{{\left( {{e^{ – 0,5}}} \right)}^x}}}{{\ln {e^{ – 0,5}}}} + C = – 2{e^{ – 0,5x}} + C\).
c) \(\int {{2^{x – 1}}.{5^{2{\rm{x}} + 1}}dx} = \int {{2^x}{{.2}^{ – 1}}.{5^{2{\rm{x}}}}.{5^1}dx} = \int {\frac{5}{2}{{.50}^x}dx} = \frac{5}{2}.\frac{{{{50}^x}}}{{\ln 50}} + C\).
Bài tập 3. Tìm:
a) \(\int {\frac{{{{\cos }^2}x}}{{1 – \sin x}}dx} \);
b) \(\int {\left( {1 + 3{{\sin }^2}\frac{x}{2}} \right)dx} \);
c) \(\int {\frac{{2{{\cos }^3}x + 3}}{{{{\cos }^2}x}}dx} \).
Lời giải
a) \(\int {\frac{{{{\cos }^2}x}}{{1 – \sin x}}dx} = \int {\frac{{1 – {{\sin }^2}x}}{{1 – \sin x}}dx} = \int {\frac{{\left( {1 – \sin x} \right)\left( {1 + \sin x} \right)}}{{1 – \sin x}}dx} = \int {\left( {1 + \sin x} \right)dx} = x – \cos x + C\).
b) \(\int {\left( {1 + 3{{\sin }^2}\frac{x}{2}} \right)dx} = \int {\left( {1 + 3.\frac{{1 – \cos x}}{2}} \right)dx} = \int {\left( {\frac{5}{2} – \frac{3}{2}\cos x} \right)dx} = \frac{5}{2}x – \frac{3}{2}\sin x + C\).
c) \(\int {\frac{{2{{\cos }^3}x + 3}}{{{{\cos }^2}x}}dx} = \int {\left( {2\cos x + \frac{3}{{{{\cos }^2}x}}} \right)dx} = 2\sin x + 3\tan x + C\).
Bài tập 4. Tìm hàm số \(f\left( x \right)\), biết rằng:
a) \(f’\left( x \right) = 2{{\rm{x}}^3} – 4{\rm{x}} + 1,f\left( 1 \right) = 0\).
b) \(f’\left( x \right) = 5\cos x – \sin x,f\left( {\frac{\pi }{2}} \right) = 1\).
Lời giải
a) \(f\left( x \right) = \int {f’\left( x \right)dx} = \int {\left( {2{{\rm{x}}^3} – 4{\rm{x}} + 1} \right)dx} = \frac{{{{\rm{x}}^4}}}{2} – 2{{\rm{x}}^2} + x + C\)
\(f\left( 1 \right) = 0 \Leftrightarrow \frac{{{1^4}}}{2} – {2.1^2} + 1 + C = 0 \Leftrightarrow C = \frac{1}{2}\)
Vậy \(f\left( x \right) = \frac{{{{\rm{x}}^4}}}{2} – 2{{\rm{x}}^2} + x + \frac{1}{2}\).
b) \(f\left( x \right) = \int {f’\left( x \right)dx} = \int {\left( {5\cos x – \sin x} \right)dx} = 5\sin x + \cos x + C\).
\(f\left( {\frac{\pi }{2}} \right) = 1 \Leftrightarrow 5\sin \frac{\pi }{2} + \cos \frac{\pi }{2} + C = 1 \Leftrightarrow C = – 4\)
Vậy \(f\left( x \right) = 5\sin x + \cos x – 4\).
Bài tập 5. Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) đi qua điểm \(\left( {1;2} \right)\) và có hệ số góc của tiếp tuyến tại mỗi điểm \(\left( {x;f\left( x \right)} \right)\) là \(\frac{{1 – x}}{{{x^2}}}\) với \(x > 0\). Tìm hàm số \(f\left( x \right)\).
Lời giải
Theo đề bài ta có: \(f’\left( x \right) = \frac{{1 – x}}{{{x^2}}}\) với \(x > 0\) và \(f\left( 1 \right) = 2\).
\(\begin{array}{l}f\left( x \right) = \int {f’\left( x \right)dx} = \int {\frac{{1 – x}}{{{x^2}}}dx} = \int {\left( {{x^{ – 2}} – \frac{1}{x}} \right)dx} = – \frac{1}{x} – \ln {\rm{x}} + C\\f\left( 1 \right) = 2 \Leftrightarrow – \frac{1}{1} – \ln 1 + C = 2 \Leftrightarrow C = 3\end{array}\)
Vậy \(f\left( x \right) = – \frac{1}{x} – \ln {\rm{x}} + 3\).
Bài tập 6. Tìm đạo hàm của hàm số \(F\left( x \right) = \ln \left( {\sqrt {{x^2} + 4} – x} \right)\). Từ đó, tìm \(\int {\frac{1}{{\sqrt {{x^2} + 4} }}dx} \).
Lời giải
Ta có: \(F’\left( x \right) = \frac{{{{\left( {\sqrt {{x^2} + 4} – x} \right)}^\prime }}}{{\sqrt {{x^2} + 4} – x}} = \frac{{\frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} – 1}}{{\sqrt {{x^2} + 4} – x}} = \frac{{\frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} – 1}}{{\sqrt {{x^2} + 4} – x}} = \frac{{\frac{{{\rm{x}} – \sqrt {{x^2} + 4} }}{{\sqrt {{x^2} + 4} }}}}{{\sqrt {{x^2} + 4} – x}} = – \frac{1}{{\sqrt {{x^2} + 4} }}\left( {x \in \mathbb{R}} \right)\)
Do đó: \(\int {\frac{1}{{\sqrt {{x^2} + 4} }}dx} = \int {\left[ { – F’\left( x \right)} \right]dx} = – \int {F’\left( x \right)dx} = – F\left( x \right) + C = – \ln \left( {\sqrt {{x^2} + 4} – x} \right) + C\).
Bài tập 7. Một vật chuyển động thẳng dọc theo một đường thẳng (có gắn trục toạ độ \(Ox\) với độ dài đơn vị bằng 1 m). Biết rằng vật xuất phát từ vị trí ban đầu là gốc toạ độ và chuyển động với vận tốc \(v\left( t \right) = 8 – 0,4t\left( {m/s} \right)\), trong đó \(t\) là thời gian tính theo giây \(\left( {t \ge 0} \right)\).
a) Xác định toạ độ \(x\left( t \right)\) của vật tại thời điểm \(t,t \ge 0\).
b) Tại thời điểm nào thì vật đi qua gốc toạ độ (không tính thời điểm ban đầu)?
Lời giải
a) \(x\left( t \right) = \int {v\left( t \right)dt} = \int {\left( {8 – 0,4t} \right)dt} = 8t – 0,2{t^2} + C\).
Do vật xuất phát từ vị trí ban đầu là gốc toạ độ nên \(x\left( 0 \right) = 0 \Leftrightarrow 8.0 – {0,2.0^2} + C = 0 \Leftrightarrow C = 0\).
Vậy \(x\left( t \right) = 8t – 0,2{t^2}\).
b) Vật đi qua gốc toạ độ khi \(x\left( t \right) = 0 \Leftrightarrow 8t – 0,2{t^2} = 0 \Leftrightarrow t = 0\) hoặc \(t = 40\).
Vậy vật đi qua gốc toạ độ tại thời điểm \(t = 40\) giây (không tính thời điểm ban đầu).
Bài tập 8. Một quần thể vi sinh vật có tốc độ tăng số lượng cá thể được ước lượng bởi \(P’\left( t \right) = 150\sqrt t \) (cá thể/ngày) với \(0 \le t \le 10\), trong đó \(P\left( t \right)\) là số lượng cá thể vi sinh vật tại thời điểm \(t\) ngày kể từ thời điểm ban đầu. Biết rằng ban đầu quần thể có 1000 cá thể.
a) Xác định hàm số \(P\left( t \right)\).
b) Ước lượng số cá thể của quần thể sau 5 ngày kể từ thời điểm ban đầu (kết quả làm tròn đến hàng trăm).
Lời giải
a) \(P\left( t \right) = \int {P’\left( t \right)dt} = \int {150\sqrt t dt} = \int {150{t^{\frac{1}{2}}}dt} = 150.\frac{{{t^{\frac{3}{2}}}}}{{\frac{3}{2}}} + C = 100t\sqrt t + C\).
Theo đề bài ta có \(P\left( 0 \right) = 1000 \Leftrightarrow 100.0\sqrt 0 + C = 1000 \Leftrightarrow C = 1000\)
Vậy \(P\left( t \right) = 100t\sqrt t + 1000\).
b) \(P\left( 5 \right) = 100.5\sqrt 5 + 1000 = 500\sqrt 5 + 1000 \approx 2100\) (cá thể).
4.2 Bài tập trắc nghiệm
Bài tập 1. Tìm nguyên hàm của hàm số \(f(x) = {\sin ^3}x.\sin 3x\).
A. $\int {f(x)dx = \frac{3}{8}\left( {\frac{{\sin 2x}}{2} – \frac{{\sin 4x}}{4}} \right) – \frac{1}{8}\left( {x – \frac{{\sin 6x}}{6}} \right) + C} $.
B. $\int {f(x)dx = \frac{3}{8}\left( {\frac{{\sin 2x}}{2} – \frac{{\sin 4x}}{4}} \right) + \frac{1}{8}\left( {x – \frac{{\sin 6x}}{6}} \right) + C} $.
C. $\int {f(x)dx = \frac{1}{8}\left( {\frac{{\sin 2x}}{2} – \frac{{\sin 4x}}{4}} \right) – \frac{3}{8}\left( {x – \frac{{\sin 6x}}{6}} \right) + C} $.
D. $\int {f(x)dx = \frac{3}{8}\left( {\frac{{\sin 2x}}{2} + \frac{{\sin 4x}}{4}} \right) – \frac{1}{8}\left( {x + \frac{{\sin 6x}}{6}} \right) + C} $.
Lời giải
\(\begin{array}{l}\int {{{\sin }^3}x.\sin 3xdx} = \int {\frac{{3\sin x – \sin 3x}}{4}.\sin 3xdx} \\ = \frac{3}{8}\int {2\sin x.\sin 3xdx} – \frac{1}{8}\int {2{{\sin }^2}3xdx} = \frac{3}{8}\int {\left( {\cos 2x – \cos 4x} \right)dx} – \frac{1}{8}\int {\left( {1 – \cos 6x} \right)dx} \\ = \frac{3}{8}\left( {\frac{{\sin 2x}}{2} – \frac{{\sin 4x}}{4}} \right) – \frac{1}{8}\left( {x – \frac{{\sin 6x}}{6}} \right) + C\end{array}\)
Bài tập 2. Tìm nguyên hàm của hàm số \(f(x) = {2^x}{.3^{ – 2{\rm{x}}}}\).
A. \(\int {f\left( x \right)d{\rm{x}}} = {\left( {\frac{2}{9}} \right)^x}.\frac{1}{{\ln 2 – \ln 9}} + C\).
B. \(\int {f\left( x \right)d{\rm{x}}} = {\left( {\frac{9}{2}} \right)^x}.\frac{1}{{\ln 2 – \ln 9}} + C\).
C. \(\int {f\left( x \right)d{\rm{x}}} = {\left( {\frac{2}{3}} \right)^x}.\frac{1}{{\ln 2 – \ln 9}} + C\).
D. \(\int {f\left( x \right)d{\rm{x}}} = {\left( {\frac{2}{9}} \right)^x}.\frac{1}{{\ln 2 + \ln 9}} + C\).
Lời giải
\(\int {{2^x}{{.3}^{ – 2{\rm{x}}}}d{\rm{x}} = \int {{{\left( {\frac{2}{9}} \right)}^x}d{\rm{x}} = } } {\left( {\frac{2}{9}} \right)^x}.\frac{1}{{\ln 2 – \ln 9}} + C\)
Bài tập 3. Một nguyên hàm \(F(x)\) của hàm số \(f(x) = {({e^{ – x}} + {e^x})^2}\) thỏa mãn điều kiện \(F(0) = 1\) là
A. \(F(x) = – \frac{1}{2}{e^{ – 2x}} + \frac{1}{2}{e^{2x}} + 2x + 1\).
B. \(F(x) = – 2{e^{ – 2x}} + 2{e^{2x}} + 2x + 1\).
C. \(F(x) = – \frac{1}{2}{e^{ – 2x}} + \frac{1}{2}{e^{2x}} + 2x\).
D. \(F(x) = – \frac{1}{2}{e^{ – 2x}} + \frac{1}{2}{e^{2x}} + 2x – 1\).
Lời giải
Ta có\(F(x) = – \frac{1}{2}{e^{ – 2x}} + \frac{1}{2}{e^{2x}} + 2x + C,F(0) = 1 \Leftrightarrow C = 1\)
Bài tập 4. Tìm nguyên hàm của hàm số \(f(x) = \frac{1}{{\sqrt {3 – x} }}\).
A. \(\int {f\left( x \right)d{\rm{x}}} = – 2\sqrt {3 – x} + C\).
B. \(\int {f\left( x \right)d{\rm{x}}} = – \sqrt {3 – x} + C\).
C. \(\int {f\left( x \right)d{\rm{x}}} = 2\sqrt {3 – x} + C\).
D. \(\int {f\left( x \right)d{\rm{x}}} = – 3\sqrt {3 – x} + C\).
Lời giải
\(\int {\frac{1}{{\sqrt {3 – x} }}d{\rm{x}} = – \int {\frac{{d\left( {3 – x} \right)}}{{\sqrt {3 – x} }} = – 2\sqrt {3 – x} + C} } \).
Bài tập 5. Tìm nguyên hàm của hàm số \(f\left( x \right) = \sqrt {{e^{3{\rm{x}}}}} \).
A. \(\int {f\left( x \right)d{\rm{x}}} = \frac{{2\sqrt {{e^{3{\rm{x}}}}} }}{3} + C\)
B. \(\int {f\left( x \right)d{\rm{x}}} = \frac{3}{{2\sqrt {{e^{3{\rm{x}}}}} }} + C\)
C. \(\int {f\left( x \right)d{\rm{x}}} = \frac{{3\sqrt {{e^{3{\rm{x}}}}} }}{2} + C\)
D. \(\int {f\left( x \right)d{\rm{x}}} = \frac{{2{e^{\frac{{3{\rm{x}} + 2}}{2}}}}}{{3{\rm{x}} + 2}} + C\)
Lời giải
\(\int {\sqrt {{e^{3{\rm{x}}}}} d{\rm{x}} = \frac{2}{3}\int {{e^{\frac{{3{\rm{x}}}}{2}}}.d\left( {\frac{{3{\rm{x}}}}{2}} \right) = \frac{2}{3}.{e^{\frac{{3{\rm{x}}}}{2}}} + C = \frac{{2\sqrt {{e^{3{\rm{x}}}}} }}{3} + C} } \)
Bài tập 6.Tìm nguyên hàm của hàm số \(f(x) = \frac{x}{{\sqrt {3{x^2} + 2} }}\).
A. \(\int {f\left( x \right)d{\rm{x}}} = \frac{1}{3}\sqrt {3{{\rm{x}}^2} + 2} + C\).
B. \(\int {f\left( x \right)d{\rm{x}}} = – \frac{1}{3}\sqrt {3{{\rm{x}}^2} + 2} + C\).
C. \(\int {f\left( x \right)d{\rm{x}}} = \frac{1}{6}\sqrt {3{{\rm{x}}^2} + 2} + C\).
D. \(\int {f\left( x \right)d{\rm{x}}} = \frac{2}{3}\sqrt {3{{\rm{x}}^2} + 2} + C\).
Lời giải
\(\int {\frac{x}{{\sqrt {3{{\rm{x}}^2} + 2} }}d{\rm{x}}} = \frac{1}{6}\int {\frac{{d\left( {3{{\rm{x}}^2} + 2} \right)}}{{\sqrt {3{{\rm{x}}^2} + 2} }} = \frac{1}{3}\sqrt {3{{\rm{x}}^2} + 2} + C} \)
Bài tập 7. Tính \(F(x) = \int {\sqrt {{x^2} – 1} dx} \) bằng:
A. \(F\left( x \right) = \frac{1}{2}x\sqrt {{x^2} – 1} – \frac{1}{2}\ln \left| {x + \sqrt {{x^2} – 1} } \right| + C\).
B. \(F\left( x \right) = \frac{1}{2}x\sqrt {{x^2} – 1} + \frac{1}{2}\ln \left| {x + \sqrt {{x^2} – 1} } \right| + C\).
C. \(F\left( x \right) = \frac{1}{2}x\sqrt {{x^2} – 1} – \frac{1}{2}\ln \left| {x – \sqrt {{x^2} – 1} } \right| + C\).
D. \(F\left( x \right) = \frac{1}{2}x\sqrt {{x^2} – 1} + \frac{1}{2}\ln \left| {x – \sqrt {{x^2} – 1} } \right| + C\).
Lời giải
Cách 1: Sử dụng định nghĩa \(F'(x) = f(x) \Leftrightarrow F'(x) – f(x) = 0\)
Nhập máy tính \(\frac{d}{{dx}}\left( {F(x)} \right) – f(x)\). CALC \(x\) tại một số giá trị ngẫu nhiên trong tập xác định, nếu kết quả xấp xỉ bằng0 thì chọn.
Cách 2: Đặt \(u = \sqrt {{x^2} – 1} ,dv = dx\) ta được\(F(x) = x\sqrt {{x^2} – 1} – F(x) – J(x)\)
với \(J(x) = \int {\frac{{dx}}{{\sqrt {{x^1} – 1} }}} \), bằng cách đặt \(u = x + \sqrt {{x^2} – 1} \) ta được \(J(x) = \ln \left| {x + \sqrt {{x^2} – 1} } \right| + C\)
Vậy \(F(x) = \frac{1}{2}x\sqrt {{x^2} – 1} – \frac{1}{2}\ln \left| {x + \sqrt {{x^2} – 1} } \right| + C\).