Nguyên hàm lượng giác là một chủ đề quan trọng trong kỳ thi tốt nghiệp THPT Quốc gia, xuất hiện nhiều trong các bài toán tích phân và ứng dụng. Việc nắm vững nguyên hàm của các hàm số lượng giác như \(\sin x\), \(\cos x\), \(\tan x\), \(\cot x\) giúp học sinh giải quyết nhanh chóng các bài toán từ cơ bản đến nâng cao, đồng thời giảm thiểu sai sót khi làm bài.
1. Công thức nguyên hàm lượng giác
Nguyên hàm lượng giác có tổng cộng 14 công thức quan trọng cần nhớ, các công thức được sắp xếp từ dễ tới khó tạo thành bảng công thức dưới đây:

2. Bài tập
Bài tập 1. Tìm: \(\int {\left( { – \frac{{\cos x}}{4}} \right)dx} \)
Lời giải
\(\int {\left( { – \frac{{\cos x}}{4}} \right)dx} = – \frac{1}{4}\int {\cos xdx} = – \frac{1}{4}\sin x + C\)
Bài tập 2. Tìm nguyên hàm \( F(x) \) của hàm số \( f(x) = \cos^2 \frac{x}{2} \)
Lời giải
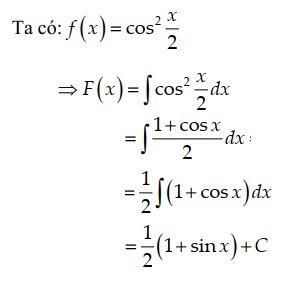
Bài tập 3. Tìm: \(\int {\left( {\frac{3}{{{{\cos }^2}x}} – \frac{1}{{{{\sin }^2}x}}} \right)dx} \)
Lời giải
$\int {\left( {\frac{3}{{{{\cos }^2}x}} – \frac{1}{{{{\sin }^2}x}}} \right)dx} $ $ = 3\int {\frac{1}{{{{\cos }^2}x}}dx} – \int {\frac{1}{{{{\sin }^2}x}}dx} $ $ = 3\tan x – \left( { – \cot x} \right) + C$
\( = 3\tan x + \cot x + C\)
Bài tập 4. Tìm họ nguyên hàm của hàm số \( f(x) = \cos x + 6x \)
Lời giải
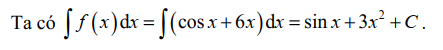
Bài tập 5. Tìm: \(\int {{{\left( {\sin \frac{x}{2} – \cos \frac{x}{2}} \right)}^2}} dx\);
Lời giải
\(\int {{{\left( {\sin \frac{x}{2} – \cos \frac{x}{2}} \right)}^2}} dx = \int {\left( {{{\sin }^2}\frac{x}{2} + {{\cos }^2}\frac{x}{2} – 2\sin \frac{x}{2}.\cos \frac{x}{2}} \right)} dx = \int {\left( {1 – \sin x} \right)} dx\)
\( = \int {dx} – \int {\sin x} dx = x + \cos x + C\)
Bài tập 6. Cho hàm số \( f(x) = \frac{1}{x} + \sin x \). Hãy tìm họ nguyên hàm của hàm số.
Lời giải
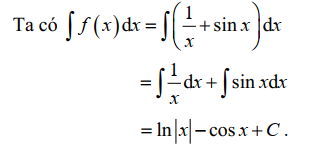
Bài tập 7. Tìm \(\int {\left( {5\cos x – 3\sin x} \right)dx} \)
Lời giải
\(\int {\left( {5\cos x – 3\sin x} \right)dx} = 5\int {\cos xdx} – 3\int {\sin xdx} = 5\sin x – 3\left( { – \cos x} \right) + C\)
\( = 5\sin x + 3\cos x + C\)
Bài tập 8. Tính I = ∫sin2x.cos4x dx
Lời giải
Áp dụng bảng nguyên hàm lượng giác ở trên:
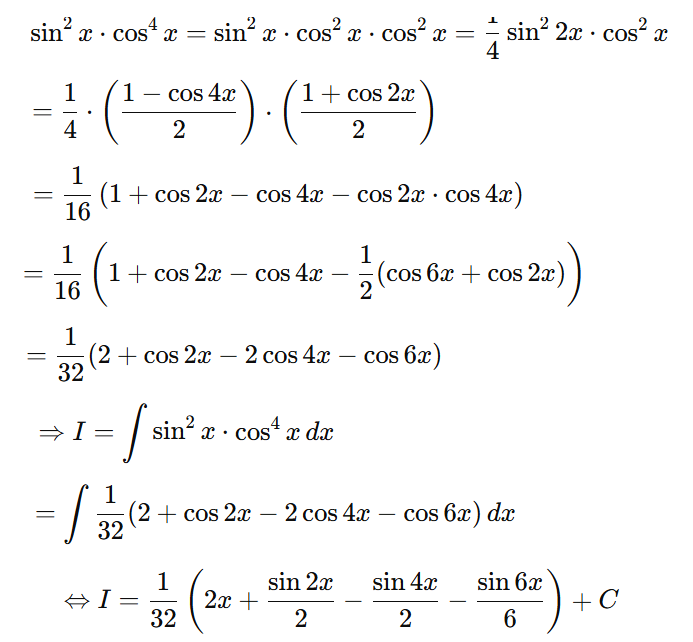
Bài tập 9. Tìm \(\int {{{\tan }^2}xdx} \)
Lời giải
$\int {{{\tan }^2}xdx} $ $ = \int {\left( {\frac{1}{{{{\cos }^2}x}} – 1} \right)dx} $ $ = \int {\frac{1}{{{{\cos }^2}x}}dx} – \int {dx} $ $ = \tan x – x + C$
Việc nắm vững công thức, phương pháp tính toán và vận dụng linh hoạt vào các bài toán giúp học sinh rèn luyện tư duy logic, nâng cao kỹ năng giải quyết vấn đề. Để đạt kết quả tốt, cần có phương pháp học tập hiệu quả, luyện tập thường xuyên và không ngừng trau dồi kiến thức. Khi làm chủ nguyên hàm lượng giác, học sinh sẽ tự tin chinh phục các bài toán tích phân và hiểu rõ hơn về các công thức nguyên hàm, góp phần đạt thành tích cao trong kỳ thi quan trọng này.