Nguyên hàm từng phần là kỹ thuật quan trọng trong toán học THPT, đặc biệt với học sinh muốn giải tốt bài thi tốt nghiệp THPT Quốc gia. Để học giỏi nguyên hàm và chinh phục đề thi, việc nắm chắc phương pháp này là cần thiết, đòi hỏi cả lý thuyết lẫn kỹ năng phân tích. Bài viết này sẽ làm rõ tại sao luyện tập nguyên hàm từng phần giúp học sinh tự tin hơn.
1. Phương pháp nguyên hàm từng phần
Cho hai hàm số \( u = u(x) \) và \( v = v(x) \) có đạo hàm liên tục trên \( K \), ta có công thức nguyên hàm từng phần: $ \int u dv = uv – \int v du. $
Chú ý: Ta thường sử dụng phương pháp nguyên hàm từng phần nếu nguyên hàm có dạng $ I = \int f(x) \cdot g(x) \, dx, $ trong đó \( f(x) \) và \( g(x) \) là 2 trong 4 hàm số: Hàm số logarit, hàm số đa thức, hàm số lượng giác, hàm số mũ.
Để tính nguyên hàm \( \int f(x) \cdot g(x) \, dx \) từng phần ta làm như sau:
- Bước 1. Đặt $ \begin{cases} u = f(x) \\ dv = g(x) \, dx \end{cases} \Rightarrow \begin{cases} du = f'(x) \, dx \\ v = G(x) \end{cases} $ (trong đó \( G(x) \) là một nguyên hàm bất kỳ của hàm số \( g(x) \))
- Bước 2. Khi đó theo công thức nguyên hàm từng phần ta có: $ \int f(x) \cdot g(x) \, dx = f(x) \cdot G(x) – \int G(x) \cdot f'(x) \, dx. $
Chú ý: Khi \( I = \int f(x) \cdot g(x) \, dx \) và \( f(x) \), \( g(x) \) là 2 trong 4 hàm số: Hàm số logarit, hàm số đa thức, hàm số lượng giác, hàm số mũ ta đặt theo quy tắc đặt \( u \).
Tức là hàm số nào đứng trước trong câu nói trên ta sẽ đặt \( u \) bằng hàm đó. Ví dụ:
- Nếu \( f(x) \) là hàm log, \( g(x) \) là một trong 3 hàm còn lại, ta sẽ đặt $ \begin{cases} u = f(x) \\ dv = g(x) \, dx \end{cases} . $
- Tương tự nếu \( f(x) \) là hàm mũ, \( g(x) \) là hàm đa thức, ta sẽ đặt $ \begin{cases} u = g(x) \\ dv = f(x) \, dx \end{cases} . $
Một số dạng nguyên hàm từng phần thường gặp.

2. Bài tập
Bài tập 1. Hãy tìm nguyên hàm sau $I = \int {{x^2}\ln x} dx$
Lời giải
Đặt $ \begin{cases} u = \ln x \\ x^2 dx = dv \end{cases} \Longleftrightarrow \begin{cases} du = \frac{dx}{x} \\ v = \frac{x^3}{3} \end{cases} $
$ \Rightarrow I = \int {{x^2}} \ln x{\mkern 1mu} {\kern 1pt} dx$ $ = \frac{{{x^3}}}{3}\ln x – \int {\frac{{{x^3}}}{3}} \cdot \frac{{dx}}{x}$ $ = \frac{{{x^3}}}{3}\ln x – \frac{{{x^3}}}{9} + C.$
Bài tập 2. Cho hàm số ${f(x) = \frac{{\ln (x – 1)}}{{{{(2x + 1)}^2}}}}$. Hãy tìm nguyên hàm của nó
Lời giải
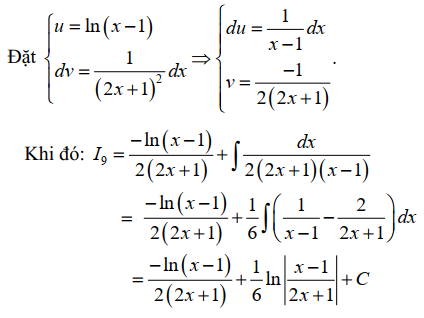
Bài tập 3. Tìm nguyên hàm của hàm số $f\left( x \right) = x\ln ({x^2} + 1)$
Lời giải
Đặt $ \begin{cases} u = \ln (1 + x^2) \\ x dx = dv \end{cases} \Rightarrow \begin{cases} du = \frac{2x dx}{1 + x^2} \\ v = \frac{x^2 + 1}{2} \end{cases} $
$ \Rightarrow I_{13} = \int x \ln (1 + x^2) \, dx = \frac{x^2 + 1}{2} \ln (1 + x^2) – \int \frac{x^2 + 1}{2} \cdot \frac{2x}{1 + x^2} \, dx. $
$ = \frac{x^2 + 1}{2} \ln (1 + x^2) – \int x \, dx. $
$ \Rightarrow I_{13} = \frac{x^2 + 1}{2} \ln (1 + x^2) – \frac{x^2}{2} + C. $
$ = \frac{(x^2 + 1) \ln (1 + x^2)}{2} – x^2 + C. $
Bài tập 4. Tìm nguyên hàm của hàm số sau $I = \int x {\tan ^2}x{\mkern 1mu} {\kern 1pt} dx$
Lời giải
\( I_{14} = \int x \tan^2 x \, dx = \int x \left(1 – \frac{1}{\cos^2 x}\right) \, dx = \int x \, dx – \int \frac{x}{\cos^2 x} \, dx \)
Tạ định \( J = \int \frac{x}{\cos^2 x} \, dx \). Đặt \(\begin{cases} u = x \\ du = dx \end{cases}\) và \(\begin{cases} dv = \frac{1}{\cos^2 x} \, dx \\ v = \tan x \end{cases}\)
$ \Rightarrow J = x\tan x – \int {\tan } x{\mkern 1mu} {\kern 1pt} dx$ $ = x\tan x – \int {\frac{{\sin x}}{{\cos x}}} {\mkern 1mu} {\kern 1pt} dx$ $ = x\tan x + \int {\frac{{d(\cos x)}}{{\cos x}}} $ $ = x\tan x + \ln |\cos x| + C$
\(\Rightarrow I_{14} = \frac{x^2}{2} + x \tan x + \ln|\cos x| + C\)
Bài tập 5. Cho nguyên hàm $ \int x \cos^2 x \, dx = m x^2 + n x \sin 2x + p \cos 2x + C $ trong đó \( m, n, p, C \in \mathbb{R} \). Tính giá trị của $ P = m + n + p. $
Lời giải
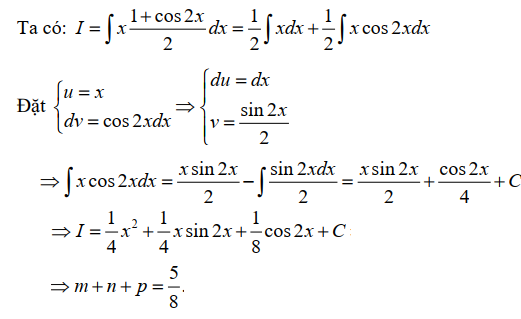
Bài tập 6. Cho $ F(x) = \left( 1 – \frac{x^2}{2} \right) \cos x + x \sin x $ là một nguyên hàm của hàm số \( f(x) \sin x \). Nguyên hàm của hàm số \( f'(x) \cos x \)?
Lời giải
Đặt $ \begin{cases} u = \cos x \\ dv = f'(x) dx \end{cases} \Rightarrow \begin{cases} du = -\sin x \, dx \\ v = f(x) \end{cases} $
$ \Rightarrow I = f(x) \cos x + \int f(x) \sin x \, dx = f(x) \cos x + \left( 1 – \frac{x^2}{2} \right) \cos x + x \sin x. $
Mặt khác $ F'(x) = -x \cos x – \left( 1 – \frac{x^2}{2} \right) \sin x + x \cos x = \frac{x^2}{2} \sin x = f(x) \sin x. $
Do đó $ f(x) = \frac{x^2}{2} $ $ \Rightarrow I = \cos x + x \sin x. $
Qua bài viết này, rõ ràng nguyên hàm từng phần là chìa khóa để học sinh giải tốt các bài toán nguyên hàm và đạt kết quả cao trong kỳ thi tốt nghiệp THPT Quốc gia. Phương pháp này không chỉ rèn tư duy phân tích mà còn mở đường cho các chủ đề nâng cao. Vì vậy, học sinh cần luyện tập chăm chỉ để nắm vững phương pháp này, đảm bảo thành công trong học tập và thi cử.