Trong chương trình toán 12, các bạn học sinh sẽ được làm quen với dạng bài về nguyên hàm hàm ẩn. Vậy chúng ta hiểu nguyên hàm hàm ẩn là gì? Hãy cùng đi tìm hiểu về khái niệm của bài toán này nhé.
Nguyên hàm hàm ẩn chính là dạng nguyên hàm mà hàm số sẽ bị ẩn đi. Hàm số đó sẽ không được biểu diễn dưới dạng là một công thức. Nguyên hàm hàm ẩn được suy ra từ tính chất nguyên hàm của hàm số:
$\int f'(x)dx – f(x) + C$
Trong công thức nguyên hàm trên, chúng ta chưa biết hệ số tự do C, sẽ biết f'(x) (hàm số bị ẩn ở trong f'(x)) nhưng sẽ biết một vài giá trị của f(x). Bài toán yêu cầu ta tính một vài giá trị khác nào đó của f(x).
1. Nguyên hàm hàm ẩn
TH1: Điều kiện của hàm ẩn có dạng
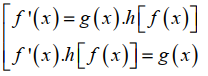
Phương pháp giải

TH2: Điều kiện hàm ẩn có dạng

Phương pháp giải

TH3: Điều kiện hàm ẩn có dạng: $ u(x) f'(x) + u'(x) f(x) = h(x) $
Phương pháp giải

2. Bài tập
Bài tập 1. Cho hàm số \( f(x) \) thỏa mãn \( f\left(\frac{\pi}{4}\right) = 0 \) và $ f'(x) \sin^2 \frac{x}{2} \cos^2 \frac{x}{2} = 1. $ Tính \( f\left(\frac{\pi}{2}\right) \).
Lời giải
Ta có: $ f'(x) \sin^2 \frac{x}{2} \cos^2 \frac{x}{2} = 1 $
$ \Rightarrow f'(x) = \frac{1}{\sin^2 \frac{x}{2} \cos^2 \frac{x}{2}} $
$ \Rightarrow f'(x) = \frac{1}{\frac{1}{4} \sin^2 x} $
$ \Rightarrow f(x) = 4 \int \frac{1}{\sin^2 x} dx $
$ \Rightarrow f(x) = 4 \cot x + C $
Do \( f\left(\frac{\pi}{4}\right) = 0 \Rightarrow C = -4 \) $ \Rightarrow f(x) = 4 \cot x – 4 $
Mà \( f\left(\frac{\pi}{2}\right) = 4 \cot \frac{\pi}{2} – 4 = 0 \).
Bài tập 2. Cho hàm số \( y = f(x) \) thỏa mãn \( f'(x) \cdot f(x) = x^4 + x^2 \). Biết \( f(0) = 2 \). Tính \( f^2(2) \).
Lời giải
Ta có \( \int f'(x) \cdot f(x) \, dx = \int (x^4 + x^2) \, dx + C \Rightarrow \frac{f^2(x)}{2} = \frac{x^5}{5} + \frac{x^3}{3} + C \).
Do \( f(0) = 2 \) nên suy ra \( C = 2 \).
Vậy \( f^2(2) = 2 \left( \frac{32}{5} + \frac{8}{3} + 2 \right) = \frac{332}{15} \).
Bài tập 3. Cho hàm số \( y = f(x) \) có đạo hàm liên tục trên đoạn \( [-2;1] \) thỏa mãn \( f(0) = 3 \) và $ (f(x))^2 \cdot f'(x) = 3x^2 + 4x + 2. $ Giá trị \( f(1) \) là?
Lời giải
Ta có: $ (f(x))^2 \cdot f'(x) = 3x^2 + 4x + 2 \quad () $
Lấy nguyên hàm 2 vế của phương trình trên ta được: $ \int (f(x))^2 \cdot f'(x)dx = \int (3x^2 + 4x + 2)dx $
$ \Leftrightarrow \int (f(x))^2 \, d(f(x)) = x^3 + 2x^2 + 2x + C $
$ \Leftrightarrow \frac{(f(x))^3}{3} = x^3 + 2x^2 + 2x + C $
$ \Leftrightarrow (f(x))^3 = 3(x^3 + 2x^2 + 2x + C) \quad (1) $
Theo đề bài \( f(0) = 3 \), nên từ (1) ta có:
$ (f(0))^3 = 3(0^3 + 2.0^2 + 2.0 + C) $
$ \Leftrightarrow 27 = 3C \Leftrightarrow C = 9 $
$ \Rightarrow (f(x))^3 = 3(x^3 + 2x^2 + 2x + 9) $
$ \Rightarrow f(x) = \sqrt[3]{3(x^3 + 2x^2 + 2x + 9)} $
$ \Rightarrow f(1) = \sqrt[3]{42} $
Bài tập 4. Cho hàm số \( f(x) \) thỏa mãn \( f(2) = -\frac{1}{25} \) và \( f'(x) = 4x^3 \left[ f(x) \right]^2 \) với mọi \( x \in \mathbb{R} \). Giá trị của \( f(1) \) bằng bao nhiêu?
Lời giải

Bài tập 5. Cho hàm số \( f(x) > 0 \) xác định và liên tục trên \( \mathbb{R} \) đồng thời thỏa mãn \( f(0) = \frac{1}{2} \), \( f'(x) = -e^x f^2(x), \ \forall x \in \mathbb{R} \). Tính giá trị của \( f(\ln 2) \).
Lời giải
