Nguyên hàm đổi biến số là một trong những chủ đề quan trọng và đầy thách thức trong chương trình toán học bậc trung học phổ thông, đặc biệt đối với học sinh chuẩn bị cho kỳ thi tốt nghiệp THPT Quốc gia. Để học tốt các khái niệm về nguyên hàm và đạt kết quả cao trong bài thi, việc nắm vững kỹ thuật đổi biến số không chỉ là một lựa chọn mà là một yêu cầu thiết yếu. Chủ đề này không chỉ đòi hỏi sự hiểu biết sâu sắc về lý thuyết mà còn rèn luyện kỹ năng tư duy linh hoạt, khả năng biến đổi bài toán một cách sáng tạo – những yếu tố then chốt để giải quyết các bài tập phức tạp.
1. Phương pháp nguyên hàm đổi biến số
1.1 Đổi biến hàm số vô tỉ
Dạng 1: Đổi biến hàm số vô tỷ đơn giản
Nguyên hàm \( \int f(x)dx \) trong đó \( f(x) = \sqrt[n]{g(x)} \) ta đặt \( t = \sqrt[n]{g(x)} \Rightarrow t^n = g(x) \)
\( \Rightarrow nt^{n-1} dt = g'(x) dx \). Khi đó \( \int f(x)dx = \int h(t) dt \).
Dạng 2: Nguyên hàm dạng \( \int f(a^x) dx \).
Ta đặt \( t = a^x \Rightarrow dt = a^x \ln a dx \Rightarrow dx = \frac{dt}{t \ln a} \Rightarrow \int f(a^x) dx = \int \frac{f(t) dt}{t \ln a} \).
Dạng 3: Nguyên hàm dạng \( \int \frac{f(\ln x)}{x} dx \).
Ta đặt \( t = \ln x \Rightarrow dt = \frac{1}{x} dx \). Khi đó \( \int \frac{f(\ln x)}{x} dx = \int f(t) dt \).
1.2 Đổi biến hàm số hữu tỉ
Dạng 1: Nếu \( f(x) \) có chứa \( \sqrt{a^2 – x^2} \), ta đặt \( x = a\sin t \), với \( t \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \).
$ dx = a\cos t \, dt $ $ \sqrt{a^2 – a^2 \sin^2 t} = |a| \cos t $
Dạng 2: Dạng \( \sqrt{x^2 + a^2} \), thì đổi biến số \( x = a \tan t \), với \( t \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) \).
$ dx = \frac{a dt}{\cos^2 t} $ $ \sqrt{a^2 + x^2} = \sqrt{a^2 + a^2 \tan^2 t} = \frac{|a|}{\cos t} $
Dạng 3: Dạng \( \sqrt{x^2 – a^2} \), thì ta đặt \( x = \frac{a}{\sin t} \) (hoặc \( x = \frac{a}{\cos t} \)).
$ dx = \frac{-a \cos t \, dt}{\sin^2 t} $ $ \sqrt{x^2 – a^2} = \frac{a}{\sin t} \cot t $
Dạng 4: Dạng \( \int \frac{dx}{x^2 + a^2} \), thì ta đặt \( x = a \tan t \).
Dạng 5: Nếu \( f(x) \) có chứa \( \sqrt{\frac{a + x}{a – x}} \), thì đặt \( x = a \cos 2t \).
$ dx = d(a \cos 2t) = -2a \sin 2t \, dt $ $ \sqrt{\frac{a + x}{a – x}} = \sqrt{\frac{1 + \cos 2t}{1 – \cos 2t}} = \sqrt{\frac{\cos^2 t}{\sin^2 t}} $
Một số kết quả quan trọng cần lưu ý khi giải trắc nghiệm:
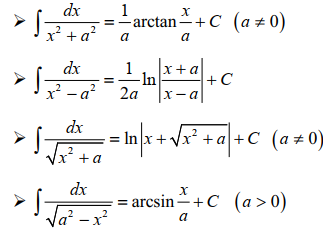
2. Bài tập
Bài tập 1. \( I = \int x^3 \sqrt{x^2 + 4} \,dx \).
Lời giải
Đặt \( t = \sqrt{x^2 + 4} \Rightarrow t^2 = x^2 + 4 \Rightarrow 2t dt = 2x dx \Leftrightarrow t dt = x dx \).
Khi đó $ I = \int x^2 \sqrt{x^2 + 4} \,dx = \int (t^2 – 4)t \,dt = \int (t^4 – 4t^2) \,dt $
$ = \frac{t^5}{5} – \frac{4t^3}{3} + C = \frac{(x^2 + 4)^{\frac{5}{2}}}{5} – \frac{4(x^2 + 4)^{\frac{3}{2}}}{3} + C. $
Bài tập 2.Hãy tìm nguyên hàm \( I = \int \frac{dx}{\sqrt{4 – x^2}} \), với \( a = 2 \).
Lời giải
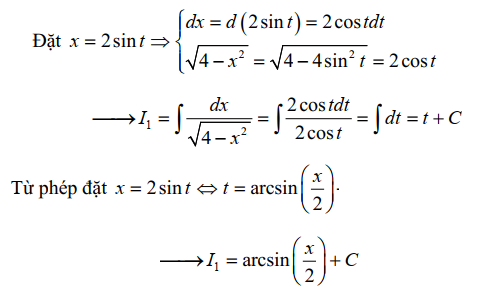
Bài tập 3. Hãy tìm nguyên hàm sau: \( I = \int x \sqrt{(x^2 + 4)^3} \,dx \).
Lời giải
Đặt \( t = \sqrt{x^2 + 4} \Rightarrow t^2 = x^2 + 4 \Rightarrow 2t dt = 2x dx \Leftrightarrow t dt = x dx \).
Khi đó $ I = \int x \sqrt{(x^2 + 4)^3} \,dx = \int t^3 t \,dt = \int t^4 \,dt $
$ = \frac{t^5}{5} + C = \frac{\sqrt{(x^2 + 4)^5}}{5} + C. $
Bài tập 4. Bằng phương pháp đổi biến số hãy tính nguyên hàm sau: \( I = \int \sqrt{1 – x^2} \, dx \), với \( a = 1 \).
Lời giải
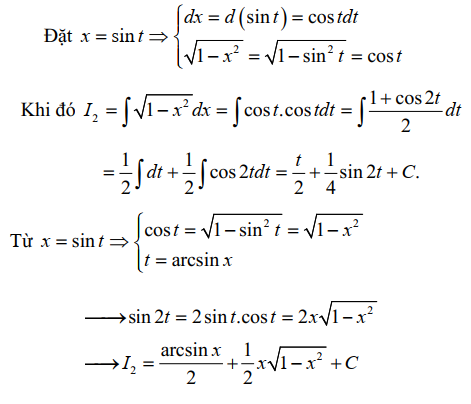
Bài tập 5. Tìm nguyên hàm của hàm số sau \( I = \int \frac{dx}{x(1 + \sqrt{x})} \).
Lời giải
Đặt \( t = \sqrt{x} \Rightarrow t^2 = x \Rightarrow 2t dt = dx \).
Khi đó
$ I = \int \frac{2t dt}{t^2 (1+t)} = \int \frac{2dt}{t (t+1)} = \int 2 \left( \frac{t+1 – t}{t (t+1)} \right) dt $
$ = 2 \left( \int \left( \frac{1}{t} – \frac{1}{t+1} \right) dt \right). $
$ = 2 \ln |t| – 2 \ln |t+1| + C = 2 \ln \left| \frac{t}{t+1} \right| + C = 2 \ln \left| \frac{\sqrt{x}}{\sqrt{x} + 1} \right| + C. $
Bài tập 6. Hãy tìm nguyên hàm sau \( I = \int \frac{x^2 dx}{\sqrt{1 – x^2}} \), với \( a = 1 \).
Lời giải
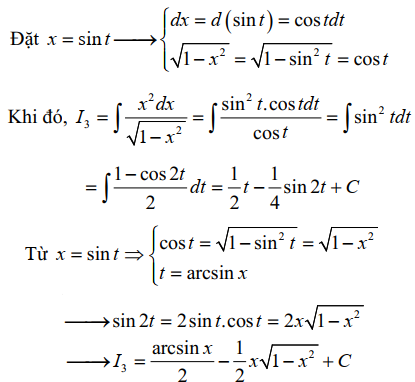
Bài tập 7. Hãy tìm nguyên hàm vô tỷ \( I = \int \frac{1}{x\sqrt{x^3 + 9}} \,dx \).
Lời giải
Đặt \( t = \sqrt{x^3 + 9} \Rightarrow t^2 = x^3 + 9 \Rightarrow 2t dt = 3x^2 dx \).
Ta có:
$ I = \int \frac{1}{x\sqrt{x^3 + 9}} dx = \int \frac{3x^2}{3x^3 \sqrt{x^3 + 9}} dx = \int \frac{2t dt}{3(t^2 – 9)t} $
$ = \frac{2}{3} \int \frac{dt}{t^2 – 9} = \frac{2}{3} \int \frac{dt}{(t-3)(t+3)} = \frac{1}{9} \int \left( \frac{(t+3) – (t-3)}{(t-3)(t+3)} \right) dt $
$ = \frac{1}{9} \int \left( \frac{1}{t-3} – \frac{1}{t+3} \right) dt. $
$ = \frac{1}{9} \ln \left| \frac{t-3}{t+3} \right| + C = \frac{1}{9} \ln \left| \frac{\sqrt{x^3 + 9} – 3}{\sqrt{x^3 + 9} + 3} \right| + C. $
Kết thúc bài viết, có thể khẳng định nguyên hàm đổi biến số là chìa khóa quan trọng giúp học sinh giải tốt các bài toán nguyên hàm, đặc biệt trong kỳ thi tốt nghiệp THPT Quốc gia. Chủ đề này không chỉ rèn tư duy linh hoạt mà còn là nền tảng để chinh phục các khái niệm nâng cao. Vì vậy, học sinh cần luyện tập nghiêm túc để nắm vững kỹ thuật này, mở ra con đường thành công trong học tập và thi cử.