Nguyên hàm của hàm số mũ là một chủ đề quan trọng với nhiều công thức cần ghi nhớ. Bài viết này sẽ hệ thống đầy đủ kiến thức cùng phương pháp giải, giúp các em tiếp thu dễ dàng và ôn tập hiệu quả. Để làm tốt dạng bài này, các em cần nắm vững những công thức cơ bản dưới đây.
1. Kiến thức nguyên hàm của hàm số mũ cần nhớ
1.1 Nguyên hàm cơ bản của hàm số e mũ
Với công thức của hàm e mũ cơ bản thì có 5 công thức cần nhớ sau đây:
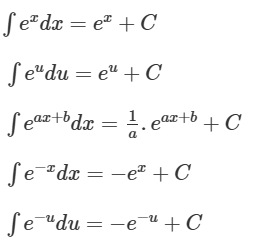
1.2 Nguyên hàm hợp của hàm số mũ
Với dạng bài liên quan tới hàm số mũ thì có 5 công thức quan trọng cần nhớ: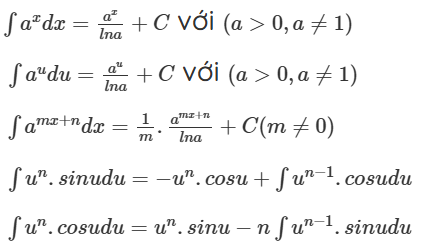
Nguyên hàm của hàm số mũ
1.2 Nguyên hàm hợp của hàm số e mũ
Hàm kết hợp của hàm số e mũ có 4 công thức nguyên hàm cần nhớ:
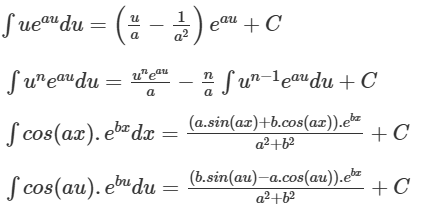
2. Bài tập
Bài tập 1. Cho hàm số e mũ có dạng \( y = e^{2x – 1} \). Tìm nguyên hàm của nó.
Lời giải
$ \int e^{2x – 1} \,dx = \frac{1}{2} \int e^{2x – 1} \,d(2x – 1) = \frac{1}{2} e^{2x – 1} + C. $
Bài tập 2. Tất cả các nguyên hàm của hàm số \( f(x) = 3^{-x} \) là
Lời giải
$\int f (x){\mkern 1mu} {\kern 1pt} dx$ $ = \int {{3^{ – x}}} {\mkern 1mu} {\kern 1pt} dx$ $ = \int {{{({3^{ – 1}})}^x}} {\mkern 1mu} {\kern 1pt} d(x)$ $ = \frac{{{3^{ – x}}}}{{\ln {3^{ – 1}}}} + C$ $ = – \frac{{{3^{ – x}}}}{{\ln 3}} + C$
Bài tập 3. Tìm nguyên hàm của hàm số \( f(x) = e^x \left( 2017 – \frac{2018e^{-x}}{x^5} \right) \).
Lời giải
$\int f (x)dx = \int {{e^x}} \left( {2017 – \frac{{2018{e^{ – x}}}}{{{x^5}}}} \right)dx$ $ = \int {\left( {2017{e^x} – \frac{{2018}}{{{x^5}}}} \right)} dx$ $ = 2017{e^x} + \frac{{504.5}}{{{x^4}}} + C$
Bài tập 4. Hãy tìm nguyên hàm \( \int 3^{x+2} . 2^{2x+1} dx \).
Lời giải
$ \int 3^{x+2} . 2^{2x+1} dx = \int 3^2 . 3^x . 2 . 2^{2x} dx = 18 \int 12^x dx $
$ = 18 \frac{12^x}{\ln 12} + C = 18 \frac{12^x}{2 \ln 2 + \ln 3} + C $
Bài tập 5. Tính \( \int (3^x + 5^x)^2 dx \).
Lời giải
$ \int (3^x + 5^x)^2 dx = \int (9^x + 30^x + 25^x) dx $
$ = \frac{9^x}{\ln 9} + \frac{30^x}{\ln 30} + \frac{25^x}{\ln 25} + C $
$ = \frac{9^x}{2 \ln 3} + \frac{30^x}{\ln 5 + \ln 3 + \ln 2} + \frac{25^x}{2 \ln 5} + C $
Bài tập 6. Tìm \( a, b, c \) để \( F(x) = (ax^2 + bx + c)e^{-2x} \) là một nguyên hàm của hàm số $ f(x) = -(2x^2 – 8x + 7)e^{-2x}. $
Lời giải

Nguyên hàm của hàm số mũ là một chủ đề quan trọng trong giải tích, không chỉ giúp củng cố nền tảng toán học mà còn là công cụ hữu ích trong nhiều bài toán thực tế. Việc nắm vững các công thức cơ bản, phương pháp biến đổi và kỹ năng xử lý linh hoạt sẽ giúp học sinh giải quyết bài toán nhanh chóng và chính xác. Hy vọng qua bài viết này, các em có thể hiểu sâu hơn về công thức nguyên hàm và áp dụng hiệu quả vào việc học tập cũng như các kỳ thi. Chúc các em học tốt!